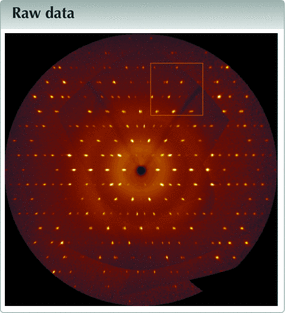
raw data letters
Accurate intensity integration in the twinned γ-form of o-nitroaniline
aDepartment of Chemistry, Structural Biochemistry, Bijvoet Centre for Biomolecular Research, Faculty of Science, Utrecht University, Utrecht, The Netherlands
*Correspondence e-mail: [email protected]
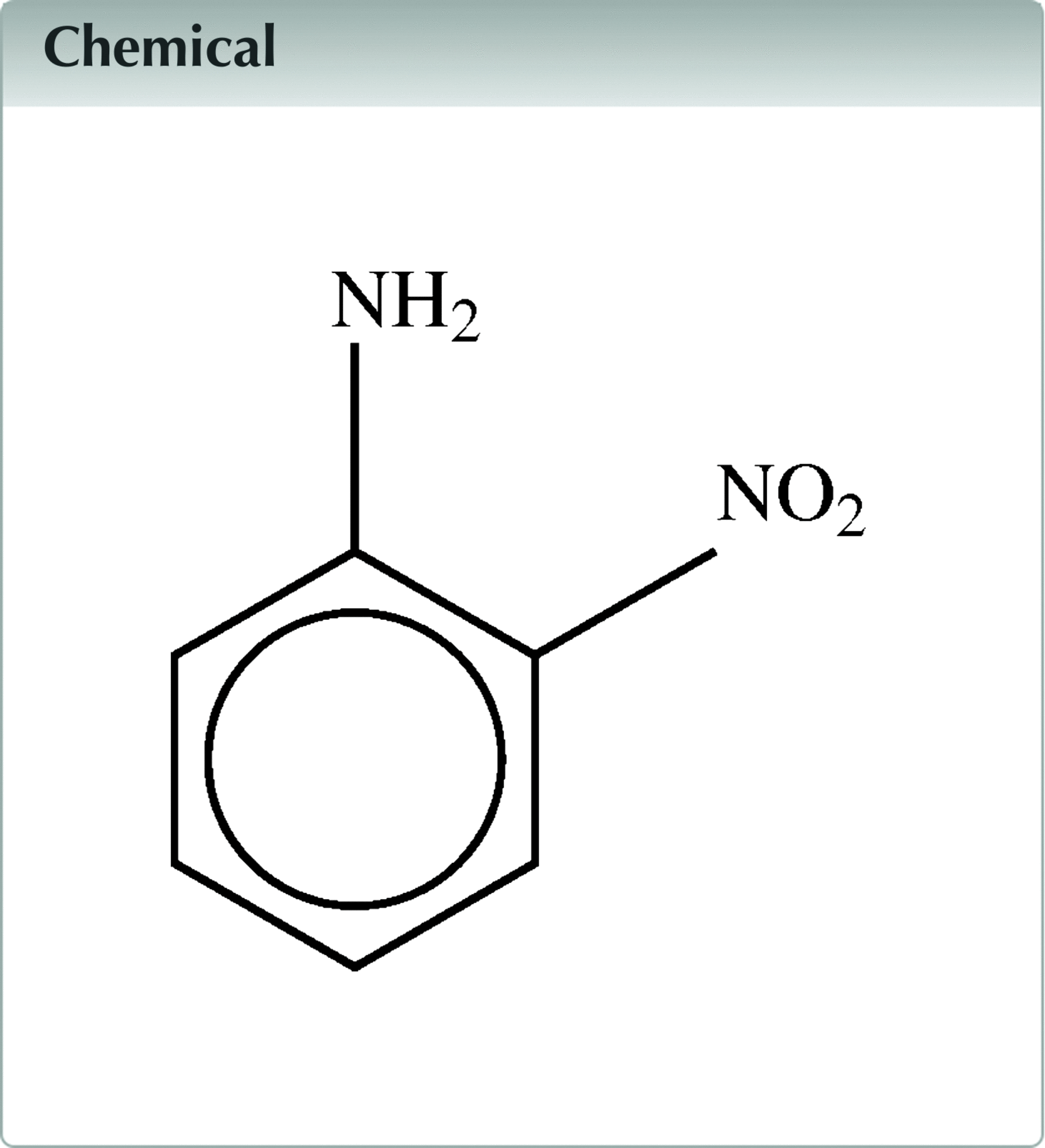
o-Nitroaniline, C6H6N2O3, is known to be polymorphic. The α-form is probably amorphous, while the β- and γ-forms are crystalline. Difficulties with the unit-cell determination of the γ-form were reported as a consequence of In this paper, newly recorded diffraction data of the γ-form of o-nitroaniline are described that were processed taking into account the two twin lattices. Data were partly deconvoluted and much better agreement was obtained in terms of R1 values and C—C bond precision. The availability of raw data and proper reprocessing using twin lattices is by far superior to efforts to de-twin processed structure factors.
Keywords: twinning; scattering; twin interface; raw data.
CCDC reference: 2217206
Metadata imgCIF file: https://doi.org/10.1107/S2414314622010598/ii4001img.cif
Introduction
o-Nitroaniline is known to be polymorphic (Aakeröy et al., 1998a![]() ,b
,b![]() ). The α-form is probably amorphous, while the β- and γ-forms are crystalline. Difficulties with the unit-cell determination of the γ-form were reported as a consequence of The appears to be C-centered orthorhombic, but was determined to be a pseudo-merohedral monoclinic twin by Herbstein (1965
). The α-form is probably amorphous, while the β- and γ-forms are crystalline. Difficulties with the unit-cell determination of the γ-form were reported as a consequence of The appears to be C-centered orthorhombic, but was determined to be a pseudo-merohedral monoclinic twin by Herbstein (1965![]() ), who also observed diffuse streaks along a*. Pseudo-orthorhombic together with unusual was discussed by Dunitz (1964
), who also observed diffuse streaks along a*. Pseudo-orthorhombic together with unusual was discussed by Dunitz (1964![]() ). While he assumed a of 0°, we here show an example where this is not exactly the case, i.e. the is 0.743°. The structure was determined before, supposedly from data of untwinned crystals, but the R1 values of 10.9, 7.01 and 7.98% remain large (Dhaneshwar et al., 1978
). While he assumed a of 0°, we here show an example where this is not exactly the case, i.e. the is 0.743°. The structure was determined before, supposedly from data of untwinned crystals, but the R1 values of 10.9, 7.01 and 7.98% remain large (Dhaneshwar et al., 1978![]() ; Nieger, 2007
; Nieger, 2007![]() ; Zych et al., 2007
; Zych et al., 2007![]() ). In this paper we describe newly recorded diffraction data of the γ-form of o-nitroaniline (I) and process these by taking into account the two twin lattices. We show that the availability of raw data and proper reprocessing using twin lattices is by far superior to efforts to de-twin processed structure factors.
). In this paper we describe newly recorded diffraction data of the γ-form of o-nitroaniline (I) and process these by taking into account the two twin lattices. We show that the availability of raw data and proper reprocessing using twin lattices is by far superior to efforts to de-twin processed structure factors.
Data processing and refinement
Data were processed in two ways: by using a single lattice, ignoring the second lattice completely, and by using two twin lattices. EVAL software (Schreurs et al., 2010![]() ) was used for both, followed by SADABS/TWINABS (Krause et al., 2015
) was used for both, followed by SADABS/TWINABS (Krause et al., 2015![]() ; Sevvana et al., 2019
; Sevvana et al., 2019![]() ) for scaling. Splitting of the radiation in Kα1 and Kα2 in a 2:1 ratio is taken into account in the EVAL model profiles for either lattice. The statistics for the two approaches are given in Table 1
) for scaling. Splitting of the radiation in Kα1 and Kα2 in a 2:1 ratio is taken into account in the EVAL model profiles for either lattice. The statistics for the two approaches are given in Table 1![]() . Several indicators in the single-crystal data processing show that the crystal is not a single crystal. The first real sign of an alarm occurs when it comes to the space-group determination: the most likely is P21/a but for the a-glide plane are clearly violated (reflection condition h0l; h = 2n). Structure with SHELXL (Sheldrick, 2015
. Several indicators in the single-crystal data processing show that the crystal is not a single crystal. The first real sign of an alarm occurs when it comes to the space-group determination: the most likely is P21/a but for the a-glide plane are clearly violated (reflection condition h0l; h = 2n). Structure with SHELXL (Sheldrick, 2015![]() ) converges at high residuals R1[I > 2σ(I)] = 0.0787 and wR2(all refl.) = 0.2545 and the proposed weighting scheme is rather unusual. The two twin lattices are related by a twofold rotation about c, resulting in the twin matrix (−1 0 −1 / 0 −1 0 / 0 0 1) (see below). With only single-crystal structure factors it is still possible to use the knowledge of the twin matrix. Inclusion of this matrix in the SHELXL assumes that the lattices overlap exactly and the obliquity would be 0°. In reality, not all reflections overlap and thus the results improve only slightly {R1[I > 2σ(I)] = 0.0678 and wR2(all refl.) = 0.2390}. As a last resort, one can de-twin the merged data with TWINROTMAT in PLATON (Spek, 2020
) converges at high residuals R1[I > 2σ(I)] = 0.0787 and wR2(all refl.) = 0.2545 and the proposed weighting scheme is rather unusual. The two twin lattices are related by a twofold rotation about c, resulting in the twin matrix (−1 0 −1 / 0 −1 0 / 0 0 1) (see below). With only single-crystal structure factors it is still possible to use the knowledge of the twin matrix. Inclusion of this matrix in the SHELXL assumes that the lattices overlap exactly and the obliquity would be 0°. In reality, not all reflections overlap and thus the results improve only slightly {R1[I > 2σ(I)] = 0.0678 and wR2(all refl.) = 0.2390}. As a last resort, one can de-twin the merged data with TWINROTMAT in PLATON (Spek, 2020![]() ). This produces an HKLF5-type file for in SHELXL in which each reflection is either overlapped or single (935 reflections are overlapping). The structure improved to R1[I > 2σ(I)] = 0.0465 and wR2(all refl.) = 0.1332. As we will see below, it is a poor approach for resolving the issue with processed data, clearly raw diffraction data are needed to reprocess with two lattices.
). This produces an HKLF5-type file for in SHELXL in which each reflection is either overlapped or single (935 reflections are overlapping). The structure improved to R1[I > 2σ(I)] = 0.0465 and wR2(all refl.) = 0.1332. As we will see below, it is a poor approach for resolving the issue with processed data, clearly raw diffraction data are needed to reprocess with two lattices.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
To show the advantage of proper processing we used two matrices. One twin component was clearly the largest and we processed the data with this lattice while including the second lattice as interfering in EVAL. Reflections are deconvoluted when the covariance of the overlapping intensities is below a given threshold. This led to 2145 overlapping and 842 single reflections and 123 (Table 1![]() ). The agreement factors of the SHELXL are much improved to R1[I > 2σ(I)] = 0.0314 and wR2(all refl.) = 0.0860 (Table 1
). The agreement factors of the SHELXL are much improved to R1[I > 2σ(I)] = 0.0314 and wR2(all refl.) = 0.0860 (Table 1![]() ) and the displacement ellipsoids of the two independent molecules are perfectly reasonable (Fig. 1
) and the displacement ellipsoids of the two independent molecules are perfectly reasonable (Fig. 1![]() ).
).
![[Figure 1]](ii4001fig1thm.gif) | Figure 1 Molecular structure of the two independent molecules of (I) in the crystal. Displacement ellipsoids are drawn at the 50% probability level. Hydrogen atoms are drawn as small spheres of arbitrary radii. The molecules are related by a non-crystallographic twofold axis approximately along a*. |
The has P21/a symmetry with two independent molecules, which are shown in Fig. 1![]() . The molecules are connected by hydrogen bonds, forming two-dimensional layers in the bc plane (Fig. 2
. The molecules are connected by hydrogen bonds, forming two-dimensional layers in the bc plane (Fig. 2![]() ).
).
![[Figure 2]](ii4001fig2thm.gif) | Figure 2 Hydrogen-bonded layers in the monoclinic structure. |
Data description
Data were collected on our in-house APEXII diffractometer with Mo Kα radiation, with multiple scans (Table 1![]() ). In total 3324 images were recorded. The was determined with DIRAX (Duisenberg, 1992
). In total 3324 images were recorded. The was determined with DIRAX (Duisenberg, 1992![]() ) and two lattices were found that could be transformed into each other with a nearly twofold rotation. Pseudo-orthorhombic is characterized by a base-centered orthorhombic derived from a monoclinic-P (Dunitz, 1964
) and two lattices were found that could be transformed into each other with a nearly twofold rotation. Pseudo-orthorhombic is characterized by a base-centered orthorhombic derived from a monoclinic-P (Dunitz, 1964![]() ). The monoclinic P cell of (I) can be transformed to a near orthorhombic B lattice [the non-standard setting of the P21/a was chosen for compatibility with earlier literature (Herbstein, 1965
). The monoclinic P cell of (I) can be transformed to a near orthorhombic B lattice [the non-standard setting of the P21/a was chosen for compatibility with earlier literature (Herbstein, 1965![]() ); base-centered B-orthorhombic was chosen so as to leave b and c unchanged] with the following operation:
); base-centered B-orthorhombic was chosen so as to leave b and c unchanged] with the following operation:
giving cell parameters a′ = 29.1340 (10), b′ = 10.0938 (4), c′ = 8.3580 (2), Å, α′ = 90, β′ = 90.743 (3), γ′ = 90°. The c axis was chosen as the twofold twin rotation axis. Clearly we find a of 0.743 (3)° and a non-merohedral twin. As a consequence, the orthorhombic B lattices of the individual twin components do not exactly overlap. If one overlooks the and indexes the spots as B-centered orthorhombic in B2212, the appear to be: hkl; h + l = 2n, 0k0; k = 2n, which is usual for the and h00; h = 4n, 00 l; l = 4n. The latter two are non-space-group and exactly such observations are considered as a signal for pseudo-orthorhombic of an underlying monoclinic lattice (Dunitz, 1964![]() ). Processing the data as single-component orthorhombic does not result in a structure solution, notably because the a glide plane is absent in B2212.
). Processing the data as single-component orthorhombic does not result in a structure solution, notably because the a glide plane is absent in B2212.
The twin rotation about the c-axis results in stacking faults of the hydrogen-bonded layers. In Fig. 3![]() , the two domains and the interface is shown. The second lattice was generated by 180° rotation around c followed by a translation over 1/2a, by which the two independent molecules are interchanged in the position. In fact, the two molecules can almost be transformed into each other by a twofold rotation along a′, the long orthorhombic axis, showing that this axis is a near orthorhombic twofold axis. The and stacking faults follow the OD theory as proposed by Dornberger-Schiff (1966
, the two domains and the interface is shown. The second lattice was generated by 180° rotation around c followed by a translation over 1/2a, by which the two independent molecules are interchanged in the position. In fact, the two molecules can almost be transformed into each other by a twofold rotation along a′, the long orthorhombic axis, showing that this axis is a near orthorhombic twofold axis. The and stacking faults follow the OD theory as proposed by Dornberger-Schiff (1966![]() ) for similar systems.
) for similar systems.
![[Figure 3]](ii4001fig3thm.gif) | Figure 3 Twin domains viewed down the monoclinic b-axis, with alternate layers colored in white, blue, green and magenta. The layers have a width of two hydrogen-bonded molecules (see Fig. 2 |
As a consequence of the ω = 0.743 (3)°, reflections are split in This can be seen in simulated precession photographs that were generated with the program PRECESSION in the EVAL package. In the 0th layers, this mainly affects layer h0l (Fig. 4![]() ). In the layers, hk0 and 0kl reflections remain nearly unaffected.
). In the layers, hk0 and 0kl reflections remain nearly unaffected.
![[Figure 4]](ii4001fig4thm.gif) | Figure 4 Left: simulated precession photograph in the h0l plane of (I) up to a resolution of 0.9 (Å). The reconstruction is based on seven scans with a total of 3324 raw images. Right: zoomed image, is from the yellow square in the left image. White circles are the predicted impacts for the first twin component, blue circles for the second. |
Supporting information
CCDC reference: 2217206
Link https://doi.org/10.5281/zenodo.7193538
Bruker SMART data files and CBF files
DOI: https://doi.org/10.1107/S2414314622010598/ii4001sup1.cif
Structure factors: contains datablock I. DOI: https://doi.org/10.1107/S2414314622010598/ii4001Isup2.hkl
Metadata imgCIF file. DOI: https://doi.org/10.1107/S2414314622010598/ii4001img.cif
CheckCIF for raw data report. DOI: https://doi.org/10.1107/S2414314622010598/ii4001img_check.pdf
Data collection: Apex3; cell Peakref; data reduction: Eval15, Twinabs; program(s) used to solve structure: SHELXS97; program(s) used to refine structure: SHELXL2018/3 (Sheldrick, 2018).
| C6H6N2O2 | F(000) = 576 |
| Mr = 138.13 | Dx = 1.493 Mg m−3 |
| Monoclinic, P21/a | Mo Kα radiation, λ = 0.71073 Å |
| a = 15.2066 (5) Å | Cell parameters from 9064 reflections |
| b = 10.0938 (4) Å | θ = 2.5–27.5° |
| c = 8.3580 (2) Å | µ = 0.12 mm−1 |
| β = 106.693 (3)° | T = 150 K |
| V = 1228.82 (7) Å3 | Block, orange |
| Z = 8 | 0.37 × 0.30 × 0.16 mm |
| Bruker Kappa APEXII Area Detector diffractometer | 2629 reflections with I > 2σ(I) |
| Radiation source: sealed tube | Rint = 0.028 |
| φ and ω scans | θmax = 27.8°, θmin = 2.5° |
| Absorption correction: multi-scan (TWINABS2012/1; Sevvana, 2019 | h = −19→19 |
| Tmin = 0.683, Tmax = 0.746 | k = −13→13 |
| 26077 measured reflections | l = −10→10 |
| 2864 independent reflections |
| Refinement on F2 | Primary atom site location: structure-invariant direct methods |
| Least-squares matrix: full | Secondary atom site location: difference Fourier map |
| R[F2 > 2σ(F2)] = 0.031 | Hydrogen site location: difference Fourier map |
| wR(F2) = 0.086 | H atoms treated by a mixture of independent and constrained refinement |
| S = 1.09 | w = 1/[σ2(Fo2) + (0.0449P)2 + 0.221P] where P = (Fo2 + 2Fc2)/3 |
| 2864 reflections | (Δ/σ)max < 0.001 |
| 198 parameters | Δρmax = 0.23 e Å−3 |
| 0 restraints | Δρmin = −0.22 e Å−3 |
Geometry. All esds (except the esd in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell esds are taken into account individually in the estimation of esds in distances, angles and torsion angles; correlations between esds in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell esds is used for estimating esds involving l.s. planes. |
Refinement. Refined as a 2-component twin. |
| x | y | z | Uiso*/Ueq | ||
| O1 | −0.03312 (6) | 0.10319 (9) | −0.14230 (11) | 0.0285 (2) | |
| O2 | 0.08962 (6) | 0.01027 (9) | −0.17072 (12) | 0.0324 (2) | |
| N1 | −0.02204 (7) | 0.31912 (12) | 0.04086 (15) | 0.0285 (2) | |
| H1 | −0.0624 (13) | 0.2625 (19) | −0.023 (2) | 0.049 (5)* | |
| H2 | −0.0380 (10) | 0.3830 (16) | 0.096 (2) | 0.027 (4)* | |
| N2 | 0.05199 (7) | 0.09765 (10) | −0.11006 (12) | 0.0218 (2) | |
| C1 | 0.06867 (8) | 0.29873 (11) | 0.06793 (13) | 0.0204 (2) | |
| C2 | 0.10796 (7) | 0.19361 (11) | −0.00104 (13) | 0.0193 (2) | |
| C3 | 0.20382 (8) | 0.17923 (12) | 0.03417 (14) | 0.0228 (2) | |
| H3 | 0.228408 | 0.106997 | −0.011917 | 0.027* | |
| C4 | 0.26139 (8) | 0.26863 (13) | 0.13415 (15) | 0.0267 (3) | |
| H4 | 0.326021 | 0.259080 | 0.158007 | 0.032* | |
| C5 | 0.22411 (8) | 0.37519 (12) | 0.20167 (15) | 0.0257 (2) | |
| H5 | 0.264081 | 0.438511 | 0.269680 | 0.031* | |
| C6 | 0.13135 (8) | 0.38906 (12) | 0.17098 (14) | 0.0237 (2) | |
| H6 | 0.108260 | 0.461106 | 0.219982 | 0.028* | |
| O3 | −0.01284 (6) | 0.39005 (10) | 0.62855 (13) | 0.0325 (2) | |
| O4 | 0.10944 (7) | 0.49706 (9) | 0.76124 (12) | 0.0344 (2) | |
| N3 | −0.00207 (8) | 0.18216 (12) | 0.44357 (14) | 0.0294 (2) | |
| H7 | −0.0423 (12) | 0.2364 (18) | 0.473 (2) | 0.045 (5)* | |
| H8 | −0.0209 (10) | 0.1190 (16) | 0.367 (2) | 0.026 (4)* | |
| N4 | 0.07189 (7) | 0.40432 (10) | 0.67046 (12) | 0.0234 (2) | |
| C7 | 0.08863 (8) | 0.20773 (12) | 0.50315 (14) | 0.0209 (2) | |
| C8 | 0.12800 (7) | 0.31208 (11) | 0.61380 (13) | 0.0196 (2) | |
| C9 | 0.22377 (8) | 0.32999 (12) | 0.67275 (14) | 0.0222 (2) | |
| H9 | 0.248337 | 0.400078 | 0.748209 | 0.027* | |
| C10 | 0.28159 (8) | 0.24690 (12) | 0.62182 (15) | 0.0251 (2) | |
| H10 | 0.346191 | 0.258978 | 0.661043 | 0.030* | |
| C11 | 0.24405 (8) | 0.14352 (12) | 0.51074 (15) | 0.0253 (2) | |
| H11 | 0.283938 | 0.086081 | 0.474351 | 0.030* | |
| C12 | 0.15120 (8) | 0.12380 (12) | 0.45380 (14) | 0.0240 (2) | |
| H12 | 0.128075 | 0.052375 | 0.379621 | 0.029* |
| U11 | U22 | U33 | U12 | U13 | U23 | |
| O1 | 0.0200 (4) | 0.0292 (4) | 0.0320 (4) | −0.0006 (3) | 0.0006 (4) | −0.0038 (4) |
| O2 | 0.0317 (4) | 0.0275 (4) | 0.0373 (5) | 0.0010 (4) | 0.0088 (4) | −0.0141 (4) |
| N1 | 0.0233 (5) | 0.0293 (5) | 0.0332 (5) | 0.0051 (4) | 0.0086 (4) | −0.0072 (5) |
| N2 | 0.0237 (4) | 0.0198 (4) | 0.0208 (4) | 0.0002 (4) | 0.0047 (4) | −0.0010 (4) |
| C1 | 0.0240 (5) | 0.0189 (5) | 0.0193 (5) | 0.0028 (4) | 0.0078 (4) | 0.0029 (4) |
| C2 | 0.0220 (5) | 0.0173 (5) | 0.0183 (5) | −0.0003 (4) | 0.0054 (4) | −0.0001 (4) |
| C3 | 0.0231 (5) | 0.0233 (5) | 0.0231 (5) | 0.0029 (4) | 0.0081 (4) | −0.0015 (4) |
| C4 | 0.0213 (5) | 0.0304 (6) | 0.0285 (6) | −0.0015 (5) | 0.0075 (5) | −0.0029 (5) |
| C5 | 0.0289 (6) | 0.0242 (6) | 0.0239 (5) | −0.0061 (5) | 0.0077 (5) | −0.0037 (5) |
| C6 | 0.0317 (6) | 0.0183 (5) | 0.0228 (5) | 0.0011 (4) | 0.0108 (5) | −0.0018 (4) |
| O3 | 0.0245 (4) | 0.0345 (5) | 0.0420 (5) | −0.0003 (4) | 0.0151 (4) | −0.0080 (4) |
| O4 | 0.0367 (5) | 0.0275 (5) | 0.0402 (5) | −0.0031 (4) | 0.0129 (4) | −0.0154 (4) |
| N3 | 0.0248 (5) | 0.0297 (5) | 0.0318 (5) | −0.0026 (4) | 0.0049 (4) | −0.0098 (5) |
| N4 | 0.0281 (5) | 0.0204 (5) | 0.0238 (5) | −0.0003 (4) | 0.0107 (4) | −0.0018 (4) |
| C7 | 0.0251 (5) | 0.0192 (5) | 0.0182 (5) | −0.0009 (4) | 0.0057 (4) | 0.0018 (4) |
| C8 | 0.0237 (5) | 0.0175 (5) | 0.0184 (5) | 0.0009 (4) | 0.0075 (4) | 0.0009 (4) |
| C9 | 0.0253 (5) | 0.0203 (5) | 0.0200 (5) | −0.0035 (4) | 0.0050 (4) | −0.0011 (4) |
| C10 | 0.0204 (5) | 0.0268 (6) | 0.0267 (5) | 0.0001 (4) | 0.0043 (4) | 0.0014 (5) |
| C11 | 0.0289 (6) | 0.0217 (5) | 0.0263 (5) | 0.0056 (4) | 0.0093 (5) | 0.0012 (5) |
| C12 | 0.0319 (6) | 0.0182 (5) | 0.0211 (5) | −0.0002 (4) | 0.0065 (5) | −0.0026 (4) |
| O1—N2 | 1.2451 (12) | O3—N4 | 1.2428 (12) |
| O2—N2 | 1.2366 (13) | O4—N4 | 1.2365 (13) |
| N1—C1 | 1.3479 (14) | N3—C7 | 1.3499 (15) |
| N1—H1 | 0.89 (2) | N3—H7 | 0.906 (18) |
| N1—H2 | 0.867 (17) | N3—H8 | 0.892 (16) |
| N2—C2 | 1.4308 (14) | N4—C8 | 1.4323 (14) |
| C1—C6 | 1.4178 (16) | C7—C8 | 1.4159 (16) |
| C1—C2 | 1.4188 (15) | C7—C12 | 1.4209 (16) |
| C2—C3 | 1.4093 (14) | C8—C9 | 1.4086 (15) |
| C3—C4 | 1.3633 (17) | C9—C10 | 1.3684 (16) |
| C3—H3 | 0.9500 | C9—H9 | 0.9500 |
| C4—C5 | 1.4073 (17) | C10—C11 | 1.4043 (17) |
| C4—H4 | 0.9500 | C10—H10 | 0.9500 |
| C5—C6 | 1.3664 (16) | C11—C12 | 1.3689 (16) |
| C5—H5 | 0.9500 | C11—H11 | 0.9500 |
| C6—H6 | 0.9500 | C12—H12 | 0.9500 |
| C1—N1—H1 | 119.9 (12) | C7—N3—H7 | 118.8 (11) |
| C1—N1—H2 | 117.0 (10) | C7—N3—H8 | 119.0 (9) |
| H1—N1—H2 | 122.8 (15) | H7—N3—H8 | 121.8 (15) |
| O2—N2—O1 | 121.19 (10) | O4—N4—O3 | 121.29 (10) |
| O2—N2—C2 | 118.90 (9) | O4—N4—C8 | 118.75 (9) |
| O1—N2—C2 | 119.91 (9) | O3—N4—C8 | 119.95 (9) |
| N1—C1—C6 | 118.74 (10) | N3—C7—C8 | 125.36 (11) |
| N1—C1—C2 | 125.17 (11) | N3—C7—C12 | 118.51 (11) |
| C6—C1—C2 | 116.08 (10) | C8—C7—C12 | 116.12 (10) |
| C3—C2—C1 | 121.55 (10) | C9—C8—C7 | 121.65 (10) |
| C3—C2—N2 | 116.98 (9) | C9—C8—N4 | 117.07 (10) |
| C1—C2—N2 | 121.47 (9) | C7—C8—N4 | 121.28 (10) |
| C4—C3—C2 | 120.22 (11) | C10—C9—C8 | 120.30 (10) |
| C4—C3—H3 | 119.9 | C10—C9—H9 | 119.8 |
| C2—C3—H3 | 119.9 | C8—C9—H9 | 119.8 |
| C3—C4—C5 | 119.34 (11) | C9—C10—C11 | 119.06 (11) |
| C3—C4—H4 | 120.3 | C9—C10—H10 | 120.5 |
| C5—C4—H4 | 120.3 | C11—C10—H10 | 120.5 |
| C6—C5—C4 | 121.06 (11) | C12—C11—C10 | 121.38 (10) |
| C6—C5—H5 | 119.5 | C12—C11—H11 | 119.3 |
| C4—C5—H5 | 119.5 | C10—C11—H11 | 119.3 |
| C5—C6—C1 | 121.72 (10) | C11—C12—C7 | 121.48 (11) |
| C5—C6—H6 | 119.1 | C11—C12—H12 | 119.3 |
| C1—C6—H6 | 119.1 | C7—C12—H12 | 119.3 |
| N1—C1—C2—C3 | −179.80 (11) | N3—C7—C8—C9 | 178.63 (11) |
| C6—C1—C2—C3 | 1.17 (15) | C12—C7—C8—C9 | −0.80 (16) |
| N1—C1—C2—N2 | 0.44 (17) | N3—C7—C8—N4 | −1.47 (17) |
| C6—C1—C2—N2 | −178.59 (10) | C12—C7—C8—N4 | 179.09 (10) |
| O2—N2—C2—C3 | −1.88 (15) | O4—N4—C8—C9 | 3.00 (15) |
| O1—N2—C2—C3 | 178.13 (10) | O3—N4—C8—C9 | −176.83 (10) |
| O2—N2—C2—C1 | 177.89 (10) | O4—N4—C8—C7 | −176.90 (10) |
| O1—N2—C2—C1 | −2.10 (16) | O3—N4—C8—C7 | 3.28 (16) |
| C1—C2—C3—C4 | −1.19 (17) | C7—C8—C9—C10 | 0.93 (17) |
| N2—C2—C3—C4 | 178.58 (11) | N4—C8—C9—C10 | −178.97 (10) |
| C2—C3—C4—C5 | 0.00 (18) | C8—C9—C10—C11 | −0.25 (17) |
| C3—C4—C5—C6 | 1.16 (18) | C9—C10—C11—C12 | −0.53 (18) |
| C4—C5—C6—C1 | −1.16 (18) | C10—C11—C12—C7 | 0.64 (18) |
| N1—C1—C6—C5 | −179.10 (11) | N3—C7—C12—C11 | −179.45 (11) |
| C2—C1—C6—C5 | −0.01 (16) | C8—C7—C12—C11 | 0.03 (16) |
| D—H···A | D—H | H···A | D···A | D—H···A |
| N1—H1···O1 | 0.89 (2) | 2.010 (19) | 2.6409 (15) | 126.4 (16) |
| N1—H2···O4i | 0.867 (17) | 2.194 (17) | 3.0345 (14) | 163.2 (14) |
| N3—H7···O3 | 0.906 (18) | 1.989 (19) | 2.6393 (15) | 127.3 (15) |
| N3—H8···O2ii | 0.892 (16) | 2.120 (16) | 3.0003 (14) | 169.0 (13) |
| Symmetry codes: (i) −x, −y+1, −z+1; (ii) −x, −y, −z. |
References
![]() Aakeröy, C. B., Nieuwenhuyzen, M. & Price, S. L. (1998a). J. Am. Chem. Soc. 120, 8986–8993. Google Scholar
Aakeröy, C. B., Nieuwenhuyzen, M. & Price, S. L. (1998a). J. Am. Chem. Soc. 120, 8986–8993. Google Scholar
![]() Aakeröy, C. B., Beatty, A. M., Nieuwenhuyzen, M. & Zou, M. (1998b). J. Mater. Chem. 8, 1385–1389. Google Scholar
Aakeröy, C. B., Beatty, A. M., Nieuwenhuyzen, M. & Zou, M. (1998b). J. Mater. Chem. 8, 1385–1389. Google Scholar
![]() Dhaneshwar, N. N., Tavale, S. S. & Pant, L. M. (1978). Acta Cryst. B34, 2507–2509. CSD CrossRef CAS IUCr Journals Web of Science Google Scholar
Dhaneshwar, N. N., Tavale, S. S. & Pant, L. M. (1978). Acta Cryst. B34, 2507–2509. CSD CrossRef CAS IUCr Journals Web of Science Google Scholar
![]() Dornberger-Schiff, K. (1966). Acta Cryst. 21, 311–322. CrossRef CAS IUCr Journals Web of Science Google Scholar
Dornberger-Schiff, K. (1966). Acta Cryst. 21, 311–322. CrossRef CAS IUCr Journals Web of Science Google Scholar
![]() Duisenberg, A. J. M. (1992). J. Appl. Cryst. 25, 92–96. CrossRef CAS Web of Science IUCr Journals Google Scholar
Duisenberg, A. J. M. (1992). J. Appl. Cryst. 25, 92–96. CrossRef CAS Web of Science IUCr Journals Google Scholar
![]() Dunitz, J. D. (1964). Acta Cryst. 17, 1299–1304. CrossRef CAS IUCr Journals Web of Science Google Scholar
Dunitz, J. D. (1964). Acta Cryst. 17, 1299–1304. CrossRef CAS IUCr Journals Web of Science Google Scholar
![]() Herbstein, F. H. (1965). Acta Cryst. 19, 590–595. CrossRef CAS IUCr Journals Web of Science Google Scholar
Herbstein, F. H. (1965). Acta Cryst. 19, 590–595. CrossRef CAS IUCr Journals Web of Science Google Scholar
![]() Krause, L., Herbst-Irmer, R., Sheldrick, G. M. & Stalke, D. (2015). J. Appl. Cryst. 48, 3–10. Web of Science CSD CrossRef ICSD CAS IUCr Journals Google Scholar
Krause, L., Herbst-Irmer, R., Sheldrick, G. M. & Stalke, D. (2015). J. Appl. Cryst. 48, 3–10. Web of Science CSD CrossRef ICSD CAS IUCr Journals Google Scholar
![]() Nieger, M. (2007). CSD Communication (CCDC No. 655336). CCDC, Cambridge, England. Google Scholar
Nieger, M. (2007). CSD Communication (CCDC No. 655336). CCDC, Cambridge, England. Google Scholar
![]() Schreurs, A. M. M., Xian, X. & Kroon-Batenburg, L. M. J. (2010). J. Appl. Cryst. 43, 70–82. Web of Science CrossRef CAS IUCr Journals Google Scholar
Schreurs, A. M. M., Xian, X. & Kroon-Batenburg, L. M. J. (2010). J. Appl. Cryst. 43, 70–82. Web of Science CrossRef CAS IUCr Journals Google Scholar
![]() Sevvana, M., Ruf, M., Usón, I., Sheldrick, G. M. & Herbst-Irmer, R. (2019). Acta Cryst. D75, 1040–1050. Web of Science CSD CrossRef ICSD IUCr Journals Google Scholar
Sevvana, M., Ruf, M., Usón, I., Sheldrick, G. M. & Herbst-Irmer, R. (2019). Acta Cryst. D75, 1040–1050. Web of Science CSD CrossRef ICSD IUCr Journals Google Scholar
![]() Sheldrick, G. M. (2015). Acta Cryst. C71, 3–8. Web of Science CrossRef IUCr Journals Google Scholar
Sheldrick, G. M. (2015). Acta Cryst. C71, 3–8. Web of Science CrossRef IUCr Journals Google Scholar
![]() Spek, A. L. (2020). Acta Cryst. E76, 1–11. Web of Science CrossRef IUCr Journals Google Scholar
Spek, A. L. (2020). Acta Cryst. E76, 1–11. Web of Science CrossRef IUCr Journals Google Scholar
![]() Zych, T., Misiaszek, T. & Szostak, M. M. (2007). Chem. Phys. 340, 260–272. Web of Science CSD CrossRef CAS Google Scholar
Zych, T., Misiaszek, T. & Szostak, M. M. (2007). Chem. Phys. 340, 260–272. Web of Science CSD CrossRef CAS Google Scholar
This is an open-access article distributed under the terms of the Creative Commons Attribution (CC-BY) Licence, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are cited.

 journal menu
journal menu





 access
access