conference papers
Lamellar crystal thickness transition of melt-crystallized isotactic polybutene-1 observed by small-angle X-ray scattering
aDepartment of Applied Chemistry, Ritsumeikan University, 1-1-1 Noji-higashi, Kusatsu, Shiga 525-8577, Japan
*Correspondence e-mail: motoi-y@is.ritsumei.ac.jp
The first-order long period L1, the second-order long period L2 and lamellar crystal thickness lc of isotactic polybutene-1 have been investigated for crystallization in the melt over a wide range (313.2 to 363.2 K) of crystallization temperatures by small-angle X-ray scattering experiments and density measurements. The long period L1 shows a single linear dependence on inverse supercooling. The crystal thickness lc, however, demonstrates two linear dependences on inverse supercooling and a transition from one dependence to the other has been observed around 338.2 K, where lc becomes comparable with the radius of gyration Rg of the samples.
Keywords: small-angle X-ray scattering; isotactic polybutene-1; tetragonal form; melt crystallization; lamellar crystal thickness.
1. Introduction
In the crystallization of polymers, polymer chains in the form of random coils develop into double layer structures composed of folded chain crystals and amorphous layers. The nucleation theory by Hoffman et al. (Hoffman et al., 1976![Hoffman, J. D., Davis, G. T. & Lauritzen, J. I. Jr (1976). Treatise on Solid State Chemistry, edited by N. B. Hannay, pp. 497-614. New York: Plenum. [Hoffman, J. D., Davis, G. T. & Lauritzen, J. I. Jr (1976). Treatise on Solid State Chemistry, edited by N. B. Hannay, pp. 497-614. New York: Plenum.]](../../../../../../logos/arrows/j_arr.gif) ; Hoffman & Miller, 1997
; Hoffman & Miller, 1997![Hoffman, J. D. & Miller, R. L. (1997). Polymer, 38, 3151-3212. [Hoffman, J. D. & Miller, R. L. (1997). Polymer, 38, 3151-3212.]](../../../../../../logos/arrows/j_arr.gif) ) explains that the crystal thickness of polymers is determined kinetically, and gives the observed dependence of lamellar thickness lc on supercooling ΔT = Tm0−T (Tm0 is the equilibrium melting temperature, T is the crystallization temperature) by the following equation (lc shows a single linear dependence on inverse supercooling, 1/ΔT):
) explains that the crystal thickness of polymers is determined kinetically, and gives the observed dependence of lamellar thickness lc on supercooling ΔT = Tm0−T (Tm0 is the equilibrium melting temperature, T is the crystallization temperature) by the following equation (lc shows a single linear dependence on inverse supercooling, 1/ΔT):
where A and δl are constants. According to the theory, A is expressed as
Here, σe is the end-surface free energy per unit area of polymer crystals and Δhf the heat of fusion per unit volume of the crystal phase. The first term lc* = 2σeTm0/ΔhfΔT in equation (1)![[link]](../../../../../../logos/arrows/j_arr.gif) represents the minimum lamellar thickness to keep the crystal thermodynamically stable and the second term corresponds to the driving force of crystallization. Hence, long period structures and crystal thicknesses of semicrystalline polymers reflect the processes of their structure formation.
represents the minimum lamellar thickness to keep the crystal thermodynamically stable and the second term corresponds to the driving force of crystallization. Hence, long period structures and crystal thicknesses of semicrystalline polymers reflect the processes of their structure formation.
Recently, Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ) observed a deviation from the nucleation theory in the temperature dependence of the crystal thickness of isotactic polybutene-1 (it-PB1) determined from electron density correlation analysis of small-angle X-ray scattering (SAXS) profiles. They observed that two different relationships exist between crystal thickness lc and crystallization temperature T, and that a transition from one relationship to the other occurs, i.e., lc increases discontinuously accompanied by a morphological change of the crystals when lc becomes comparable to the chain dimensions. They also showed that crystals with two different kinds of thicknesses co-exist around the transition temperatures.
) observed a deviation from the nucleation theory in the temperature dependence of the crystal thickness of isotactic polybutene-1 (it-PB1) determined from electron density correlation analysis of small-angle X-ray scattering (SAXS) profiles. They observed that two different relationships exist between crystal thickness lc and crystallization temperature T, and that a transition from one relationship to the other occurs, i.e., lc increases discontinuously accompanied by a morphological change of the crystals when lc becomes comparable to the chain dimensions. They also showed that crystals with two different kinds of thicknesses co-exist around the transition temperatures.
To elucidate the influence of chain dimensions on the resultant lamellar long period structure, we have reinvestigated this transition in terms of more simple methods, using it-PB1 samples with a different molecular weight distribution from that used in the study by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ). We have studied the temperature dependence of the first- and second-order long periods and lamellar crystal thicknesses of it-PB1 tetragonal crystals grown in the melt by SAXS experiments and crystallinity measurements. it-PB1 is a semicrystalline polyolefin with ethyl side groups. it-PB1 exhibits a stable trigonal form with 3/1 helical chains and a metastable tetragonal form with 11/3 helical chains as the most common structures, as shown in Table 1
). We have studied the temperature dependence of the first- and second-order long periods and lamellar crystal thicknesses of it-PB1 tetragonal crystals grown in the melt by SAXS experiments and crystallinity measurements. it-PB1 is a semicrystalline polyolefin with ethyl side groups. it-PB1 exhibits a stable trigonal form with 3/1 helical chains and a metastable tetragonal form with 11/3 helical chains as the most common structures, as shown in Table 1![[link]](../../../../../../logos/arrows/j_arr.gif) . Crystallization in the bulk melt under atmospheric pressure yields the tetragonal form (Turner-Jones, 1963
. Crystallization in the bulk melt under atmospheric pressure yields the tetragonal form (Turner-Jones, 1963![Turner-Jones, A. (1963). J. Polym. Sci. Part B Polym. Lett. 1, 455. [Turner-Jones, A. (1963). J. Polym. Sci. Part B Polym. Lett. 1, 455.]](../../../../../../logos/arrows/j_arr.gif) ). Due to the metastability of the tetragonal form, the solid–solid spontaneous transformation to the stable trigonal form then takes place over several days after cooling to room temperature (Natta et al., 1960
). Due to the metastability of the tetragonal form, the solid–solid spontaneous transformation to the stable trigonal form then takes place over several days after cooling to room temperature (Natta et al., 1960![Natta, G., Corradini, P. & Bassi, I. W. (1960). Nuovo Cimento Suppl. 15, 52-67. [Natta, G., Corradini, P. & Bassi, I. W. (1960). Nuovo Cimento Suppl. 15, 52-67.]](../../../../../../logos/arrows/j_arr.gif) ).
).
![Miller, R. L. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 7-8. New York: Wiley Interscience. [Miller, R. L. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 7-8. New York: Wiley Interscience.]](../../../../../../logos/arrows/j_arr.gif) ). ).
‡Leute & Dollhopf (1983 ![Leute, U. & Dollhopf, W. (1983). Colloid Polym. Sci. 261, 299-305. [Leute, U. & Dollhopf, W. (1983). Colloid Polym. Sci. 261, 299-305.]](../../../../../../logos/arrows/j_arr.gif) ). ).
§Natta et al. (1960 ![Natta, G., Corradini, P. & Bassi, I. W. (1960). Nuovo Cimento Suppl. 15, 52-67. [Natta, G., Corradini, P. & Bassi, I. W. (1960). Nuovo Cimento Suppl. 15, 52-67.]](../../../../../../logos/arrows/j_arr.gif) ). ).
¶Tashiro et al. (1998 ![Tashiro, K., Saiani, A., Miyashita, S., Chatani, Y. & Tadokoro, H. (1998). Polym. Prepr. Jpn, 47, 3869-3870. [Tashiro, K., Saiani, A., Miyashita, S., Chatani, Y. & Tadokoro, H. (1998). Polym. Prepr. Jpn, 47, 3869-3870.]](../../../../../../logos/arrows/j_arr.gif) ). ).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In this study, we again confirmed the two different temperature dependences of the crystal thickness lc. We observed two linearities in the inverse supercooling dependence of lc, which indicates that each of the two relationships still obeys the nucleation theory. We also observed an abnormality in the supercooling dependence of the second-order long period around 353.2 K. We are going to discuss possible mechanisms for the transition.
2. Experimental
2.1. Lamellar crystal thickness
The it-PB1 used in this study was purchased from Scientific Polymer Products. Weight- and number-averaged molecular weights determined with gel permeation chromatography (GPC) calibrated with polystyrene standard samples are Mw = 277 300 and Mn = 60 340, respectively.
We measured the density ρ of samples by a float and sink method using mixed solvents of water and ethanol at 298.2 K; the crystallinity φ was determined from the density using
where ρc and ρa are the densities of the crystalline and amorphous phases, respectively, listed in Table 1![[link]](../../../../../../logos/arrows/j_arr.gif) .
.
SAXS photographs were taken with a SAXS camera (camera length 414 mm) in vacuum to obtain lamellar long periods, using an imaging plate system (Rigaku R-AXIS DSII). Nickel-filtered Cu Kα radiation was used, generated at 50 kV and 140 mA. After the subtraction of the background intensity, isotropic two-dimensional data were circularly averaged to obtain one-dimensional data and corrected for the Lorentz factor. The first- and second-order reflections were separated by fitting SAXS profiles with Gaussian–Lorentzian product functions. Application of Bragg's law to the scattering peak centers was used to calculate the first- and second-order long periods, L1 and L2. The lamellar crystal thickness lc was estimated using the equation lc = φL1.
Films of it-PB1 of about 500 µm thickness were sandwiched between aluminium foil and melted at 423.2 K for 3 min in an oven, transferred quickly to a hot stage (Mettler FP82) and kept at a crystallization temperature between 313.2 and 363.2 K. The films crystallized were aged at room temperature for 10 d and used for SAXS and density measurements. After 10 d of aging at room temperature, the tetragonal crystals transform into the trigonal form without changing their stacked lamellae structure and overall mass degree of crystallinity. Since the crystal density of the trigonal form is larger than that of the tetragonal form, the SAXS intensity is much enhanced after 10 d. We determined lc of the aged samples, then calculated lc of the as-crystallized tetragonal samples from the observed values of lc of the aged samples assuming that lc(as-crystallized) = lc(aged)/1.12. This assumption is based on the fact that the tetragonal–trigonal transformation involves an extension of the 11/3 helical conformation (tetragonal form) into the 3/1 helix (trigonal form). The ratio between the axial repeating units of this conformation is 1.12.
2.2. Identification of crystal structures
Wide-angle X-ray scattering (WAXS) was performed to identify crystal structures. Nickel-filtered Cu Kα radiation was used, generated at 35 kV and 40 mA. The system and procedure used for data acquisition and analysis were the same as those used for SAXS experiments.
3. Results
3.1. Crystal structures from WAXS and TEM
We confirmed by WAXS measurements that samples immediately after the crystallization are in the tetragonal form (Fig. 1![[link]](../../../../../../logos/arrows/j_arr.gif) ). Hence the observed crystallinity and lamellar crystal thickness reflect those of tetragonal crystals. Samples stored at room temperature for 10 d exhibited peaks characteristic of the trigonal form.
). Hence the observed crystallinity and lamellar crystal thickness reflect those of tetragonal crystals. Samples stored at room temperature for 10 d exhibited peaks characteristic of the trigonal form.
![[Figure 1]](sy6022fig1thm.gif)
|
Figure 1
WAXS profiles of it-PB1 crystallized at 313.2, 338.2 and 363.2 K plotted against the modulus of the scattering vector Q. (Q = 4πλ−1sin θ, θ is half the scattering angle, λ is the wavelength used.) The profiles for samples as crystallized and aged are plotted. Peaks shown in the plots of as crystallized samples are indexed with the 200, 220, 213 reflections of the tetragonal form; peaks exhibited in the plots of the aged samples are indexed with the 110, 300, 220 reflections of the trigonal form. |
3.2. Lamellar crystal thickness
Fig. 2![[link]](../../../../../../logos/arrows/j_arr.gif) shows the Lorentz-corrected SAXS profiles of the samples. First- and second-order reflections were observed in the wide range of crystallization temperatures from 313.2 to 363.2 K. Table 2
shows the Lorentz-corrected SAXS profiles of the samples. First- and second-order reflections were observed in the wide range of crystallization temperatures from 313.2 to 363.2 K. Table 2![[link]](../../../../../../logos/arrows/j_arr.gif) lists the results of SAXS and density measurements: crystallization temperatures, the values of the first- and second-order long periods, the ratios of the second-order long period to the first-order long period, the degrees of crystallinity and the lamellar crystal thicknesses.
lists the results of SAXS and density measurements: crystallization temperatures, the values of the first- and second-order long periods, the ratios of the second-order long period to the first-order long period, the degrees of crystallinity and the lamellar crystal thicknesses.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![[Figure 2]](sy6022fig2thm.gif)
|
Figure 2
SAXS profiles for it-PB1 samples crystallized at temperatures from 313.2 to 363.2 K. The profiles have been shifted vertically for clarity. |
Fig. 3![[link]](../../../../../../logos/arrows/j_arr.gif) shows the first-order long period L1 and second-order long period L2 as a function of the inverse supercooling, 1/ΔT. (ΔT = Tm0−T; the equilibrium melting temperature Tm0 is 397.2 K for the it-PB1 tetragonal phase, as given in Table 1
shows the first-order long period L1 and second-order long period L2 as a function of the inverse supercooling, 1/ΔT. (ΔT = Tm0−T; the equilibrium melting temperature Tm0 is 397.2 K for the it-PB1 tetragonal phase, as given in Table 1![[link]](../../../../../../logos/arrows/j_arr.gif) .) The 1/ΔT dependence of L1 demonstrates a single linearity over the whole temperature range investigated. For the 1/ΔT dependence of L2, on the contrary, a shoulder is observed around 1/ΔT = 0.0227, which corresponds to a crystallization temperature T = 353.2 K.
.) The 1/ΔT dependence of L1 demonstrates a single linearity over the whole temperature range investigated. For the 1/ΔT dependence of L2, on the contrary, a shoulder is observed around 1/ΔT = 0.0227, which corresponds to a crystallization temperature T = 353.2 K.
![[Figure 3]](sy6022fig3thm.gif)
|
Figure 3
The first-order long period L1 and the second-order long period L2 as a function of the inverse supercooling, 1/ΔT. |
Fig. 4![[link]](../../../../../../logos/arrows/j_arr.gif) shows the lamellar crystal thickness lc plotted against 1/ΔT. The dependence deviates from a single linearity. Two linear relationships between lc and 1/ΔT can be observed, one in the low ΔT range (1/ΔT = 0.018−0.030 K−1; this corresponds to T = 363−343 K) and the other in the high ΔT range (1/ΔT = 0.012−0.016 K−1; this corresponds to T = 333−313 K). When 1/ΔT increases from the high ΔT range to the low ΔT range, lc moves up from the lower line to the upper line in Fig. 4
shows the lamellar crystal thickness lc plotted against 1/ΔT. The dependence deviates from a single linearity. Two linear relationships between lc and 1/ΔT can be observed, one in the low ΔT range (1/ΔT = 0.018−0.030 K−1; this corresponds to T = 363−343 K) and the other in the high ΔT range (1/ΔT = 0.012−0.016 K−1; this corresponds to T = 333−313 K). When 1/ΔT increases from the high ΔT range to the low ΔT range, lc moves up from the lower line to the upper line in Fig. 4![[link]](../../../../../../logos/arrows/j_arr.gif) . This is in agreement with the observation reported by Fu et al. (2001
. This is in agreement with the observation reported by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ). At 1/ΔT = 0.017, lc lies in the middle of the two linearities, which suggests a transition state between the two linear relationships. According to equations (1)
). At 1/ΔT = 0.017, lc lies in the middle of the two linearities, which suggests a transition state between the two linear relationships. According to equations (1)![[link]](../../../../../../logos/arrows/j_arr.gif) and (2)
and (2)![[link]](../../../../../../logos/arrows/j_arr.gif) , the extrapolation to 1/ΔT = 0 K−1 of the straight lines in Fig. 4
, the extrapolation to 1/ΔT = 0 K−1 of the straight lines in Fig. 4![[link]](../../../../../../logos/arrows/j_arr.gif) gives the values of δlc to be 38.8 ± 8.4 Å for the low ΔT range and 44.3 ± 4.8 Å for the high ΔT range. The slopes give the values of 2σeTm0/Δhf to be (4.90 ± 0.39) × 103 Å K for the low ΔT range and (4.01 ± 0.35) × 103 Å K for the high ΔT range; σe is estimated as (6.73 ± 0.49) × 10−2 J m−2 for the low ΔT range and (5.51 ± 0.48) × 10−2 J m−2 for the high ΔT range, using the values of Δhf and Tm0 given in Table 1
gives the values of δlc to be 38.8 ± 8.4 Å for the low ΔT range and 44.3 ± 4.8 Å for the high ΔT range. The slopes give the values of 2σeTm0/Δhf to be (4.90 ± 0.39) × 103 Å K for the low ΔT range and (4.01 ± 0.35) × 103 Å K for the high ΔT range; σe is estimated as (6.73 ± 0.49) × 10−2 J m−2 for the low ΔT range and (5.51 ± 0.48) × 10−2 J m−2 for the high ΔT range, using the values of Δhf and Tm0 given in Table 1![[link]](../../../../../../logos/arrows/j_arr.gif) . Chain folding free energies q = 2abσe (a and b represent the height and width of a stem, respectively; the values are shown in Table 1
. Chain folding free energies q = 2abσe (a and b represent the height and width of a stem, respectively; the values are shown in Table 1![[link]](../../../../../../logos/arrows/j_arr.gif) ) are calculated as (7.17 ± 0.52) × 10−20 J stem−1 for the low ΔT range and (5.87 ± 0.51) × 10−20 J stem−1 for the high ΔT range.
) are calculated as (7.17 ± 0.52) × 10−20 J stem−1 for the low ΔT range and (5.87 ± 0.51) × 10−20 J stem−1 for the high ΔT range.
![[Figure 4]](sy6022fig4thm.gif)
|
Figure 4
Lamellar crystal thickness lc as a function of the inverse supercooling, 1/ΔT. The broken line represents the radius of gyration Rg. |
4. Discussion
First, we will discuss the temperature and crystallinity dependence of L1 and L2. For simplicity, we consider strictly periodic two-phase systems as reviewed by Strobl & Schneider (1980![Strobl, G. & Schneider, M. (1980). J. Polym. Sci. Polym. Phys. Ed. 18, 1343-1359. [Strobl, G. & Schneider, M. (1980). J. Polym. Sci. Polym. Phys. Ed. 18, 1343-1359.]](../../../../../../logos/arrows/j_arr.gif) ) and assume our crystallized samples to be composed of ensembles of many different strictly periodic structures with different long periods. A periodic structure shows an electron density distribution h(z) as indicated in Fig. 5
) and assume our crystallized samples to be composed of ensembles of many different strictly periodic structures with different long periods. A periodic structure shows an electron density distribution h(z) as indicated in Fig. 5![[link]](../../../../../../logos/arrows/j_arr.gif) (a). It can be described by specifying the long period L, the crystal thickness lc and the electron density of the crystal and amorphous phases, hc and ha. Here, and in the following, we choose a crystallinity φ = lc/L < 0.5.
(a). It can be described by specifying the long period L, the crystal thickness lc and the electron density of the crystal and amorphous phases, hc and ha. Here, and in the following, we choose a crystallinity φ = lc/L < 0.5.
![[Figure 5]](sy6022fig5thm.gif)
|
Figure 5
(a) Electron density distribution function h(z) and (b) the related correlation function K(z) for a strictly periodic two phase system. |
The correlation function K(z) is given by the following expressions:
Here Δ denotes the average range for z′. Ka(z) is calculated as follows:
Equations (4)![[link]](../../../../../../logos/arrows/j_arr.gif) and (5)
and (5)![[link]](../../../../../../logos/arrows/j_arr.gif) give the profile of K(z) as shown in Fig. 5
give the profile of K(z) as shown in Fig. 5![[link]](../../../../../../logos/arrows/j_arr.gif) (b). The scattering intensity distribution function S(Q) is given as follows:
(b). The scattering intensity distribution function S(Q) is given as follows:
In periodic systems with long period L, the first- and second-order scattering is observed where the modulus of the scattering vector Q takes values of 2π/L and 4π/L, respectively, referring to Bragg's equation λ = 2dsin θ (θ is half the scattering angle). The Lorentz-corrected first- and second-order scattering intensity is given as 4πQ2S(2π/L) and 4πQ2S(4π/L), respectively, and is readily calculated as follows:
For samples with φ > 0.5, we can apply all the equations after making the replacements of ![[\varphi \to 1 - \varphi]](teximages/sy6022fi1.gif) and
and ![[h_{\rm{c}} \leftrightarrow h_{\rm{a}}]](teximages/sy6022fi2.gif) , and we obtain
, and we obtain
This follows from Babinet's reciprocity theorem. Fig. 6![[link]](../../../../../../logos/arrows/j_arr.gif) shows the φ dependences of S(2π/L)
shows the φ dependences of S(2π/L) ![[\equiv]](teximages/sy6022fi3.gif) S1 and S(4π/L)
S1 and S(4π/L) ![[\equiv]](teximages/sy6022fi3.gif) S2. The S1 value becomes a maximum at φ = 0.5 while S2 takes a minimal value 0 at φ = 0.5.
S2. The S1 value becomes a maximum at φ = 0.5 while S2 takes a minimal value 0 at φ = 0.5.
![[Figure 6]](sy6022fig6thm.gif)
|
Figure 6
Crystallinity φ dependences of the first- and second-order scattering intensity S1 and S2. |
We then introduce a crystal thickness distribution function Fc(lc), assuming la to be a fixed value at a given temperature. The distribution function of the long period is given as FL(L) = Fc(L − la). Fc(lc) is considered to possess an asymmetric profile as given in Fig. 7![[link]](../../../../../../logos/arrows/j_arr.gif) (a), since lc has a lower bound lc* = 2σeTm0T/ΔhfΔT for lamellar crystals to keep themselves thermodynamically stable. We discuss here the scattering intensity distribution in real space L instead of Q space. The first- and second-order scattering intensity distribution from ensembles of periodic structures with many different long periods is given by S1(φ)FL(L) and S2(φ)FL(L), respectively. The peak position L′1 of S1(φ)FL(L) corresponds to the first-order scattering peak position in Q space. Hence, L′1 is equal to L1. On the other hand, if we put L′2 to be the peak position of S2(φ)FL(L), L′2/2 corresponds to the second-order peak position in Q space. Hence, L2 is equal to L′2/2. Around the range of observed φ, S1(φ) can roughly be taken to be constant and L1 is roughly equal to the peak position of FL(L). On the contrary, S2(φ) becomes close to 0 around φ = 0.5, i.e. L = 2la. Distribution of L far from L = 2la largely contributes to the second-order scattering and contribution from the range around 2la is negligible.
(a), since lc has a lower bound lc* = 2σeTm0T/ΔhfΔT for lamellar crystals to keep themselves thermodynamically stable. We discuss here the scattering intensity distribution in real space L instead of Q space. The first- and second-order scattering intensity distribution from ensembles of periodic structures with many different long periods is given by S1(φ)FL(L) and S2(φ)FL(L), respectively. The peak position L′1 of S1(φ)FL(L) corresponds to the first-order scattering peak position in Q space. Hence, L′1 is equal to L1. On the other hand, if we put L′2 to be the peak position of S2(φ)FL(L), L′2/2 corresponds to the second-order peak position in Q space. Hence, L2 is equal to L′2/2. Around the range of observed φ, S1(φ) can roughly be taken to be constant and L1 is roughly equal to the peak position of FL(L). On the contrary, S2(φ) becomes close to 0 around φ = 0.5, i.e. L = 2la. Distribution of L far from L = 2la largely contributes to the second-order scattering and contribution from the range around 2la is negligible.
![[Figure 7]](sy6022fig7thm.gif)
|
Figure 7
(a) Speculated profiles of the crystal thickness distribution function Fc(lc) at φ ≃ 0.48, (b)–(e) long period distribution functions FL(L) (solid lines) and second-order scattering intensity distribution functions S2(φ)FL(L) (broken lines) at several different crystallinity φ values. The shapes of these asymmetric functions were estimated from the function (lc − lc*)exp[−B(lc* + δl)/kT] defined in the range lc > lc*. (B is a constant.) The first factor represents the driving force of crystallization and the second factor represents the barrier for chain folding. The convergence of distribution with increasing temperature can be accounted for by the second factor. |
At φ slightly smaller than 0.5, the main part of the distribution which lies around the FL(L) peak does not contribute to the second-order scattering (Fig. 7![[link]](../../../../../../logos/arrows/j_arr.gif) b). Only the long distribution `tail' which locates in the range of L sufficiently larger than 2la > L1 contributes to L2. Hence, the second-order scattering is weak and S2(φ)FL(L) has a peak around L′2 > L′1 = L1; L2/L1 becomes larger than 1/2. With increasing crystallization temperature the crystallinity φ increases, and the distribution of L shifts to a larger value of L. The distribution, however, also converges to around L1 (Fig. 7
b). Only the long distribution `tail' which locates in the range of L sufficiently larger than 2la > L1 contributes to L2. Hence, the second-order scattering is weak and S2(φ)FL(L) has a peak around L′2 > L′1 = L1; L2/L1 becomes larger than 1/2. With increasing crystallization temperature the crystallinity φ increases, and the distribution of L shifts to a larger value of L. The distribution, however, also converges to around L1 (Fig. 7![[link]](../../../../../../logos/arrows/j_arr.gif) c). The distribution tail becomes shorter, which makes L2/L1 decrease almost monotonically toward 0.5. Around φ ≃ 0.55 (Fig. 7
c). The distribution tail becomes shorter, which makes L2/L1 decrease almost monotonically toward 0.5. Around φ ≃ 0.55 (Fig. 7![[link]](../../../../../../logos/arrows/j_arr.gif) d), the main part of the distribution of L is considered to shift to the region L > 2la. A considerable part of the distribution of L larger than L1 contributes to the second-order scattering, which makes L2/L1 larger again. This can account for the shoulder around 1/ΔT = 0.0227, which corresponds to T = 353 K. At higher crystallization temperatures, the distribution is considered to become much more converged around L1 (Fig. 7
d), the main part of the distribution of L is considered to shift to the region L > 2la. A considerable part of the distribution of L larger than L1 contributes to the second-order scattering, which makes L2/L1 larger again. This can account for the shoulder around 1/ΔT = 0.0227, which corresponds to T = 353 K. At higher crystallization temperatures, the distribution is considered to become much more converged around L1 (Fig. 7![[link]](../../../../../../logos/arrows/j_arr.gif) e). The distribution tail located at L > L1 becomes much smaller and L2/L1 approaches 1/2 again. To summarize, we can speculate that the shoulder observed in the L2 vs 1/ΔT plot is caused by the asymmetric distribution of L when it passes through 2la, converging on itself.
e). The distribution tail located at L > L1 becomes much smaller and L2/L1 approaches 1/2 again. To summarize, we can speculate that the shoulder observed in the L2 vs 1/ΔT plot is caused by the asymmetric distribution of L when it passes through 2la, converging on itself.
We next consider the transition observed in the lc vs 1/ΔT plot. We observed two different dependences of lc on 1/ΔT and the transition between them. This is consistent with the observation by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ). On the other hand, lc depends linearly on 1/ΔT in each of the low and high supercooling ranges, which is in accordance with the nucleation theory. The growth mechanisms described by the nucleation theory still seem to be working in each of the low and high supercooling ranges. Below we are going to analyze the transition according to the hypothesis proposed by Fu et al. and show that one of the results obtained in this work can not be explained by their model. Then we will present a simple model that can account for the transition.
). On the other hand, lc depends linearly on 1/ΔT in each of the low and high supercooling ranges, which is in accordance with the nucleation theory. The growth mechanisms described by the nucleation theory still seem to be working in each of the low and high supercooling ranges. Below we are going to analyze the transition according to the hypothesis proposed by Fu et al. and show that one of the results obtained in this work can not be explained by their model. Then we will present a simple model that can account for the transition.
Polymer chains are elongated along the crystal-melt interface before they become incorporated into the crystal phase. If the crystal thickness is smaller than the chain dimensions in the melt, Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ) assumed that crystallization does not necessary need a chain disentangling; the entanglements can be shifted into the amorphous regions, where they can be accumulated together with the other noncrystallizable chain parts such as end groups and stereodefects. An estimation of the chain dimensions in the melt is the radius of gyration Rg. Then, the condition for crystallization without disentangling can be obtained as follows:
) assumed that crystallization does not necessary need a chain disentangling; the entanglements can be shifted into the amorphous regions, where they can be accumulated together with the other noncrystallizable chain parts such as end groups and stereodefects. An estimation of the chain dimensions in the melt is the radius of gyration Rg. Then, the condition for crystallization without disentangling can be obtained as follows:
If this condition is not satisfied, i.e. if the crystal thickness is larger than Rg, they proposed that the chain needs to be disentangled to crystallize.
For Gaussian chains, Rg and the mean-squared end-to-end distance R0 are related by the following equation:
R0 can be calculated using the characteristic ratio ![[C_\infty]](teximages/sy6022fi6.gif) as
as
Here, ab2 represents the sum of squares of the lengths of the backbone bonds in one monomer unit and N is the degree of polymerization.
For it-PB1, ![[C_\infty]](teximages/sy6022fi6.gif) is given as 18.0 in the literature (Kurata & Tsunashima, 1999
is given as 18.0 in the literature (Kurata & Tsunashima, 1999![Kurata, M. & Tsunashima, Y. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 48-49. New York: Wiley Interscience. [Kurata, M. & Tsunashima, Y. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 48-49. New York: Wiley Interscience.]](../../../../../../logos/arrows/j_arr.gif) ); ab2 is 4.74 Å2. The value N is calculated to be 1078 from the number-averaged molecular weight and Rg is determined to be 124 Å. This value is roughly in agreement with the crystal thickness 117 Å at T = 338.2 K (1/ΔT = 0.017), which is the temperature of the crystal thickness transition observed in Fig. 4
); ab2 is 4.74 Å2. The value N is calculated to be 1078 from the number-averaged molecular weight and Rg is determined to be 124 Å. This value is roughly in agreement with the crystal thickness 117 Å at T = 338.2 K (1/ΔT = 0.017), which is the temperature of the crystal thickness transition observed in Fig. 4![[link]](../../../../../../logos/arrows/j_arr.gif) . The agreement supports the observations by Fu et al. (2001
. The agreement supports the observations by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ). The hypothesis that chain dimensions could influence the process of crystal growth seems to be right.
). The hypothesis that chain dimensions could influence the process of crystal growth seems to be right.
However, the model by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ) can not explain the change in the slope of the lc vs 1/ΔT plot. The two linearities we observed in the 1/ΔT dependence of lc also indicate that the dependences obey the nucleation theory in each of the high and low ΔT ranges. The slope of the lc vs 1/ΔT plot is proportional to the end surface free energy σe of crystals, i.e. it reflects the free energy q = 2abσe of a chain folding. The q value determined from the low ΔT range is larger than that determined from the high ΔT range by 1.30 × 10−20 J stem−1, which amounts to 22% of the q value in the high ΔT range. The difference can not be explained only by whether disentanglement of chain molecules works or not, because disentanglement itself changes neither the energy of chain folding nor the conformational entropy of polymer chain. When chains are elongated beyond Rg the envelope of the volume occupied by the chains can be elongated and deformed, causing the loss of conformational entropy of the chains. The reduced entropy, however, will be observed as the lateral surface free energy, not the end surface free energy. This can be reasonably treated within the nucleation theory (Hoffman & Miller, 1997
) can not explain the change in the slope of the lc vs 1/ΔT plot. The two linearities we observed in the 1/ΔT dependence of lc also indicate that the dependences obey the nucleation theory in each of the high and low ΔT ranges. The slope of the lc vs 1/ΔT plot is proportional to the end surface free energy σe of crystals, i.e. it reflects the free energy q = 2abσe of a chain folding. The q value determined from the low ΔT range is larger than that determined from the high ΔT range by 1.30 × 10−20 J stem−1, which amounts to 22% of the q value in the high ΔT range. The difference can not be explained only by whether disentanglement of chain molecules works or not, because disentanglement itself changes neither the energy of chain folding nor the conformational entropy of polymer chain. When chains are elongated beyond Rg the envelope of the volume occupied by the chains can be elongated and deformed, causing the loss of conformational entropy of the chains. The reduced entropy, however, will be observed as the lateral surface free energy, not the end surface free energy. This can be reasonably treated within the nucleation theory (Hoffman & Miller, 1997![Hoffman, J. D. & Miller, R. L. (1997). Polymer, 38, 3151-3212. [Hoffman, J. D. & Miller, R. L. (1997). Polymer, 38, 3151-3212.]](../../../../../../logos/arrows/j_arr.gif) ).
).
Another candidate for the mechanisms causing the change of the slope in the lc vs 1/ΔT plot is the change of chain folding manner caused by kinetic roughening. it-PB1 tetragonal crystals have a facetted morphology indicative of flat growth fronts on the molecular scale at lower ΔT, while they present a rounded morphology with a kinetically roughened growth front on the molecular scale (Yamashita et al., 2004![Yamashita, M., Miyaji, H., Izumi, K. & Hoshino, A. (2004) Polym. J. 36, 226-237. [Yamashita, M., Miyaji, H., Izumi, K. & Hoshino, A. (2004) Polym. J. 36, 226-237.]](../../../../../../logos/arrows/j_arr.gif) , 2007
, 2007![Yamashita, M., Hoshino, A. & Kato, M. (2007). J. Polym. Sci. Part B Polym. Phys. 45, 684-697. [Yamashita, M., Hoshino, A. & Kato, M. (2007). J. Polym. Sci. Part B Polym. Phys. 45, 684-697.]](../../../../../../logos/arrows/j_arr.gif) ). In facetted crystals of the tetragonal phase, the chain folding direction is restricted to that parallel to the (100) growth front within each (100) sector since step propagation occurs along the (100) growth front during the crystallization process. A chain can fold from one site in the lattice to its two adjacent sites along the (100) plane. On the contrary, in kinetically roughened crystals, the chain folding direction is no longer restricted to (100) directions; a chain can fold into at least eight neighboring sites. With increasing temperature, the growth front changes from rounded to facetted morphology, which reduces the number of re-entrant sites from eight to two. Reduced re-entrant sites cause the reduction of the configurational entropy of the re-entrant sites and the conformational entropy of a folded chain, and these factors could account for the difference between the chain folding free energy values. The entropy of chain re-entrant sites for facetted and kinetically roughened growth fronts are estimated to be kln 2 stem−1 and kln 8 stem−1, respectively; the reduction of chain re-entrant sites is calculated to be 2kln 2. This corresponds to the free energy difference of 6.47 × 10−21 J stem−1 at 338.2 K. This value is half the difference between the q values, 13.0 × 10−21 J stem−1; if we assume the reduction of the conformational entropy to have the same order of magnitude as that of the configurational entropy of re-entrant sites, we can explain the difference between the q values.
). In facetted crystals of the tetragonal phase, the chain folding direction is restricted to that parallel to the (100) growth front within each (100) sector since step propagation occurs along the (100) growth front during the crystallization process. A chain can fold from one site in the lattice to its two adjacent sites along the (100) plane. On the contrary, in kinetically roughened crystals, the chain folding direction is no longer restricted to (100) directions; a chain can fold into at least eight neighboring sites. With increasing temperature, the growth front changes from rounded to facetted morphology, which reduces the number of re-entrant sites from eight to two. Reduced re-entrant sites cause the reduction of the configurational entropy of the re-entrant sites and the conformational entropy of a folded chain, and these factors could account for the difference between the chain folding free energy values. The entropy of chain re-entrant sites for facetted and kinetically roughened growth fronts are estimated to be kln 2 stem−1 and kln 8 stem−1, respectively; the reduction of chain re-entrant sites is calculated to be 2kln 2. This corresponds to the free energy difference of 6.47 × 10−21 J stem−1 at 338.2 K. This value is half the difference between the q values, 13.0 × 10−21 J stem−1; if we assume the reduction of the conformational entropy to have the same order of magnitude as that of the configurational entropy of re-entrant sites, we can explain the difference between the q values.
In our previous work, we determined the kinetic roughening temperature to be around 358.2 K (Yamashita et al., 2004![Yamashita, M., Miyaji, H., Izumi, K. & Hoshino, A. (2004) Polym. J. 36, 226-237. [Yamashita, M., Miyaji, H., Izumi, K. & Hoshino, A. (2004) Polym. J. 36, 226-237.]](../../../../../../logos/arrows/j_arr.gif) ). This is not in agreement with the observed temperature of the thickness transition, 338.2 K. However, we also observed (100) sector boundaries in kinetically roughened crystals at 358.2 K. The existence of sector boundaries indicates that the crystals have a considerable fraction of (100) folding even in the kinetically roughened state. This is considered to be due to the fact that the surface nucleation process is still alive and step propagation along the (100) direction is working on a kinetically roughened growth front, since the growth front is not thermally roughened. If we assume that the fraction of (100) folding undergoes a large decrease in the temperature range of 333.2–343.2 K, we can account for the transition temperature in the 1/ΔT dependence of lc. To confirm our hypothesis, we need to observe the (100) sector boundaries disappearing in this temperature range.
). This is not in agreement with the observed temperature of the thickness transition, 338.2 K. However, we also observed (100) sector boundaries in kinetically roughened crystals at 358.2 K. The existence of sector boundaries indicates that the crystals have a considerable fraction of (100) folding even in the kinetically roughened state. This is considered to be due to the fact that the surface nucleation process is still alive and step propagation along the (100) direction is working on a kinetically roughened growth front, since the growth front is not thermally roughened. If we assume that the fraction of (100) folding undergoes a large decrease in the temperature range of 333.2–343.2 K, we can account for the transition temperature in the 1/ΔT dependence of lc. To confirm our hypothesis, we need to observe the (100) sector boundaries disappearing in this temperature range.
Although the second model described above is rather trivial, it seems more probable because it can explain the change in q without any large changes in the crystallization mechanisms. Experiments on the crystallization behaviour are still insufficient to determine the mechanisms of transition. In particular, a more precise investigation of the crystallization kinetics and the morphology of growth shape in the high ΔT range is deemed necessary.
5. Conclusion
We observed the two temperature dependences of lamellar crystal thickness lc and the transition from one dependence to the other reported by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ) in the crystallization of the it-PB1 tetragonal phase with a different molecular weight by means of more simple methods. We determined the first-order long period L1 and the second-order long period L2 along with the lamellar crystal thickness lc of tetragonal crystals of it-PB1 grown in the melt from SAXS experiments and density measurements over a wide range of crystallization temperatures T from 313.2 to 363.2 K. The 1/ΔT dependence of L1 demonstrated a single linearity over the whole temperature range investigated while that of L2 showed a shoulder around 1/ΔT = 0.0227, which corresponds to T = 353.2 K. The shoulder could be attributed to the asymmetric distribution of lc converging with increasing temperature and the increase of crystallinity accompanied by increasing crystallization temperature. The dependence of lc on 1/ΔT presented two linearities and the transition from one dependence to the other was observed around T = 338.2 K, where lc becomes roughly in agreement with the radius of gyration Rg of the samples we used. Each of the two dependences obeys the nucleation theory in the high and low ΔT ranges. The chain folding free energy q determined from the low ΔT range is larger than that determined from the high ΔT range by 1.30 × 10−20 J stem−1. The model proposed by Fu et al. (2001
) in the crystallization of the it-PB1 tetragonal phase with a different molecular weight by means of more simple methods. We determined the first-order long period L1 and the second-order long period L2 along with the lamellar crystal thickness lc of tetragonal crystals of it-PB1 grown in the melt from SAXS experiments and density measurements over a wide range of crystallization temperatures T from 313.2 to 363.2 K. The 1/ΔT dependence of L1 demonstrated a single linearity over the whole temperature range investigated while that of L2 showed a shoulder around 1/ΔT = 0.0227, which corresponds to T = 353.2 K. The shoulder could be attributed to the asymmetric distribution of lc converging with increasing temperature and the increase of crystallinity accompanied by increasing crystallization temperature. The dependence of lc on 1/ΔT presented two linearities and the transition from one dependence to the other was observed around T = 338.2 K, where lc becomes roughly in agreement with the radius of gyration Rg of the samples we used. Each of the two dependences obeys the nucleation theory in the high and low ΔT ranges. The chain folding free energy q determined from the low ΔT range is larger than that determined from the high ΔT range by 1.30 × 10−20 J stem−1. The model proposed by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ) can not account for the change in the difference between the q values, while it can roughly explain the transition temperature. The difference can be roughly explained by considering the change in chain folding directions caused by kinetic roughening without any large change of crystallization mechanisms as assumed by Fu et al. (2001
) can not account for the change in the difference between the q values, while it can roughly explain the transition temperature. The difference can be roughly explained by considering the change in chain folding directions caused by kinetic roughening without any large change of crystallization mechanisms as assumed by Fu et al. (2001![Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511. [Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502-2511.]](../../../../../../logos/arrows/j_arr.gif) ).
).
Acknowledgements
The authors express their sincere thanks to Mr Masada (Tokuyama Corporation) for GPC measurements, Professor Sawamura (Ritsumeikan University) and Dr Matsuo (Ritsumeikan University) for their kind instruction in the density measurement technique, Professor Nakamura (Ritsumeikan University) for help with the instrumentation used for sample preparation, and Mr Mori (Ritsumeikan University) and Mr Kudo (Ritsumeikan University) for their kind instruction in software used for SAXS profile analysis. This work was partially supported by `Academic Frontier' Project from MEXT, 2004–2008.
References
 Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502–2511. Web of Science CrossRef CAS
Fu, Q., Heck, B., Strobl, G. & Thoman, Y. (2001). Macromolecules, 34, 2502–2511. Web of Science CrossRef CAS
 Hoffman, J. D., Davis, G. T. & Lauritzen, J. I. Jr (1976). Treatise on Solid State Chemistry, edited by N. B. Hannay, pp. 497–614. New York: Plenum.
Hoffman, J. D., Davis, G. T. & Lauritzen, J. I. Jr (1976). Treatise on Solid State Chemistry, edited by N. B. Hannay, pp. 497–614. New York: Plenum.
 Hoffman, J. D. & Miller, R. L. (1997). Polymer, 38, 3151–3212. CrossRef CAS Web of Science
Hoffman, J. D. & Miller, R. L. (1997). Polymer, 38, 3151–3212. CrossRef CAS Web of Science
 Kurata, M. & Tsunashima, Y. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 48–49. New York: Wiley Interscience.
Kurata, M. & Tsunashima, Y. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 48–49. New York: Wiley Interscience.
 Leute, U. & Dollhopf, W. (1983). Colloid Polym. Sci. 261, 299–305. CrossRef CAS Web of Science
Leute, U. & Dollhopf, W. (1983). Colloid Polym. Sci. 261, 299–305. CrossRef CAS Web of Science
 Miller, R. L. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 7–8. New York: Wiley Interscience.
Miller, R. L. (1999). Polymer Handbook, edited by J. Brandrup & E. H. Immergut, Vol. VI, pp. 7–8. New York: Wiley Interscience.
 Natta, G., Corradini, P. & Bassi, I. W. (1960). Nuovo Cimento Suppl. 15, 52–67. CrossRef CAS
Natta, G., Corradini, P. & Bassi, I. W. (1960). Nuovo Cimento Suppl. 15, 52–67. CrossRef CAS
 Starkweather, H. W. Jr & Jones, G. A. (1986). J. Polym. Sci. Part B Polym. Phys. 24, 1509–1514. CrossRef CAS Web of Science
Starkweather, H. W. Jr & Jones, G. A. (1986). J. Polym. Sci. Part B Polym. Phys. 24, 1509–1514. CrossRef CAS Web of Science
 Strobl, G. & Schneider, M. (1980). J. Polym. Sci. Polym. Phys. Ed. 18, 1343–1359. CrossRef CAS Web of Science
Strobl, G. & Schneider, M. (1980). J. Polym. Sci. Polym. Phys. Ed. 18, 1343–1359. CrossRef CAS Web of Science
 Tashiro, K., Saiani, A., Miyashita, S., Chatani, Y. & Tadokoro, H. (1998). Polym. Prepr. Jpn, 47, 3869–3870.
Tashiro, K., Saiani, A., Miyashita, S., Chatani, Y. & Tadokoro, H. (1998). Polym. Prepr. Jpn, 47, 3869–3870.
 Turner-Jones, A. (1963). J. Polym. Sci. Part B Polym. Lett. 1, 455.
Turner-Jones, A. (1963). J. Polym. Sci. Part B Polym. Lett. 1, 455.
 Yamashita, M., Hoshino, A. & Kato, M. (2007). J. Polym. Sci. Part B Polym. Phys. 45, 684–697. CrossRef CAS
Yamashita, M., Hoshino, A. & Kato, M. (2007). J. Polym. Sci. Part B Polym. Phys. 45, 684–697. CrossRef CAS
 Yamashita, M., Miyaji, H., Izumi, K. & Hoshino, A. (2004) Polym. J. 36, 226–237. Web of Science CrossRef CAS
Yamashita, M., Miyaji, H., Izumi, K. & Hoshino, A. (2004) Polym. J. 36, 226–237. Web of Science CrossRef CAS
© International Union of Crystallography. Prior permission is not required to reproduce short quotations, tables and figures from this article, provided the original authors and source are cited. For more information, click here.


 journal menu
journal menu
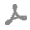




![[l_{\rm c} = {A \over {\Delta T}} + \delta l \equiv l_{\rm c} ^* + \delta l, \eqno (1)]](teximages/sy6022fd1.gif)
![[A = {{2\sigma _{\rm{e}} T_{\rm m}^0} \over {\Delta h_{\rm f}}}, \eqno (2)]](teximages/sy6022fd2.gif)
![[\bar{R}3c]](teximages/sy6022fi9.gif)
![[\bar{P}4b2]](teximages/sy6022fi10.gif)
![[\rho = \rho _{\rm c} \varphi + \rho _{\rm a} (1 - \varphi), \eqno (3)]](teximages/sy6022fd3.gif)
![[\eqalign{ & K(z) = \ K_{\rm a} (z) - (\langle h \rangle - h_{\rm a})^2 \cr & K_{\rm a} (z) = \int_{ - \Delta /2}^{\Delta /2} {\left[h(z') - h_{\rm a}\right] \left[h(z' + z) - h_{\rm a}\right] } {\rm d}z'. \cr} \eqno (4)]](teximages/sy6022fd4.gif)
![[\eqalign{\matrix{K_{\rm a} (z) = (h_{\rm c} - h_{\rm a})^2 (d - z)/L &{\rm if }\, \, \left| z \right| \,\,\lt d \cr \kern-50pt = 0 &\,\,\,\,{\rm if}\,\, d \lt \left| z \right| \lt \left| {L - d} \right| \cr \,\,\, K_{\rm a} (z + L) = K_{\rm a} (z). \cr}} \eqno (5)]](teximages/sy6022fd5.gif)
![[S(Q) = {2 \over {4\pi Q^2 }}(2\pi)^2 \int_{ - \infty }^\infty {\exp (iQz)K(z)} {\rm d}z. \eqno (6)]](teximages/sy6022fd6.gif)
![[\eqalign{ & S\left({{{2\pi } \over L}} \right) \propto {1 - \cos \left({2\pi {{l_{\rm{c}} } \over L}} \right)} = 1 - \cos 2\pi \varphi \equiv S_1 (\varphi) \cr & S\left({{{4\pi } \over L}} \right) \propto {1 - \cos \left({4\pi {{l_{\rm c} } \over L}} \right)} = 1 - \cos 4\pi \varphi \equiv S_2 (\varphi). \cr} \eqno (7)]](teximages/sy6022fd7.gif)
![[\eqalign{ & S\left({{{2\pi } \over L}} \right) \propto {1 - \cos \left({2\pi {{L - l_{\rm c} } \over L}} \right)} = 1 - \cos [2\pi (1 - \varphi)] \equiv S_1 (\varphi) \cr & S\left({{{4\pi } \over L}} \right) \propto {1 - \cos \left({4\pi {{L - l_{\rm c} } \over L}} \right)} = 1 - \cos [4\pi (1 - \varphi)] \equiv S_2 (\varphi). \cr} \eqno (8)]](teximages/sy6022fd8.gif)
![[l_{\rm c} \le R_{\rm g}. \eqno (9)]](teximages/sy6022fd9.gif)
![[R_{\rm g}^2 = {{R_0^2 } \over 6}. \eqno (10)]](teximages/sy6022fd10.gif)
![[R_{\rm 0}^2 = C_\infty a_{\rm b}^2 N. \eqno (11)]](teximages/sy6022fd11.gif)